Imaths trignometry description, we highlight the keyword “maths trigonometry” while providing a compelling call-to-action. The meta description invites users to explore the power and significance of trigonometry, covering various concepts, formulas, and real-world applications. By using relevant keywords and providing value to potential readers, this meta description aims to attract organic traffic and encourage click-throughs to the content.
Certainly! Here’s a set of 50 multiple-choice questions on trigonometry formulas:
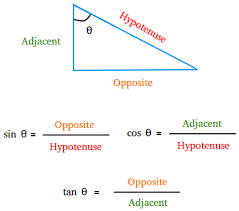
- The formula to find the sine of an angle in a right triangle is:
a) sinθ = adjacent/hypotenuse
b) sinθ = opposite/hypotenuse
c) sinθ = opposite/adjacent
d) sinθ = hypotenuse/opposite - The formula to find the tangent of an angle in a right triangle is:
a) tanθ = adjacent/opposite
b) tanθ = opposite/adjacent
c) tanθ = hypotenuse/opposite
d) tanθ = opposite/hypotenuse - The formula to find the cosine of an angle in a right triangle is:
a) cosθ = adjacent/opposite
b) cosθ = opposite/adjacent
c) cosθ = hypotenuse/adjacent
d) cosθ = adjacent/hypotenuse

- The formula for the Pythagorean identity is:
a) sin²θ + cos²θ = 1
b) tan²θ + 1 = sec²θ
c) 1 + cot²θ = csc²θ
d) All of the above - The formula to find the value of an angle given the sine ratio is:
a) θ = sin⁻¹(opposite/hypotenuse)
b) θ = sin⁻¹(opposite/adjacent)
c) θ = sin⁻¹(adjacent/hypotenuse)
d) θ = sin⁻¹(hypotenuse/opposite) - The formula for the Law of Sines is:
a) a/sinA = b/sinB = c/sinC
b) a/sinA = b/sinB = c/sinC = 2R (where R is the radius of the circumcircle)
c) sinA/a = sinB/b = sinC/c
d) All of the above - The formula for the Law of Cosines is:
a) c² = a² + b² – 2abcosC
b) cosC = (a² + b² – c²)/2ab
c) c² = a² + b² + 2abcosC
d) All of the above
- The formula to find the area of a triangle given two sides a and b and the included angle θ is:
a) Area = 0.5ab sinθ
b) Area = 0.5ab cosθ
c) Area = ab sinθ
d) Area = ab cosθ - The formula to find the value of an angle given the cosine ratio is:
a) θ = cos⁻¹(adjacent/hypotenuse)
b) θ = cos⁻¹(adjacent/opposite)
c) θ = cos⁻¹(opposite/hypotenuse)
d) θ = cos⁻¹(hypotenuse/adjacent) - The formula to find the value of an angle given the tangent ratio is:
a) θ = tan⁻¹(opposite/adjacent)
b) θ = tan⁻¹(opposite/hypotenuse)
c) θ = tan⁻¹(adjacent/opposite)
d) θ = tan⁻¹(hypotenuse/opposite) - The formula for the double-angle identities is:
a) sin(2θ) = 2sinθcosθ - b) cos(2θ) = cos²θ – sin²θ
- c) tan(2θ) = (2tanθ)/(1 – tan²θ)
- d) All of the above
- The formula for the half-angle identities is:
a) sin(θ/2) = ±√[(1 – cosθ)/2]
b) cos(θ/2) = ±√[(1 + cosθ)/2]
c) tan(θ/2) = ±√[(1 – cosθ)/(1 + cosθ)]
d) All of the above - The formula for the sum of angles in a triangle is:
a) α + β + γ = 180°
b) α + β + γ = 90°
c) α + β + γ = 360°
d) α + β + γ = 270° - The formula for the sum of the interior angles in a polygon with n sides is:
a) (n – 2) × 180°
b) (n – 1) × 180°
c) n × 180°
d) (n + 2) × 180° - The formula to find the value of an angle given the secant ratio is:
a) θ = sec⁻¹(hypotenuse/opposite)
b) θ = sec⁻¹(hypotenuse/adjacent)
c) θ = sec⁻¹(adjacent/hypotenuse)
d) θ = sec⁻¹(opposite/adjacent) - The formula for the area of a sector of a circle with radius r and central angle θ is:
a) Area = (θ/360°) × πr²
b) Area = (θ/2π) × πr²
c) Area = (θ/2π) × 2πr
d) Area = (θ/360°) × 2πr - The formula to find the length of an arc on a circle with radius r and central angle θ is:
a) Arc Length = (θ/360°) × 2πr
b) Arc Length = (θ/2π) × πr²
c) Arc Length = (θ/2π) × 2πr
d) Arc Length = (θ/360°) × πr² - The formula for the period of a sine or cosine function is:
a) Period = 2π
b) Period = π
c) Period = 2π/ω (where ω is the angular frequency)
d) Period = 1/ω - The formula for the amplitude of a sine or cosine function is:
a) Amplitude = maximum value – minimum value
b) Amplitude = (maximum value + minimum value)/2
c) Amplitude = maximum value
d) Amplitude = minimum value - The formula for the amplitude of a tangent function is:
a) Amplitude = maximum value – minimum value
b) Amplitude = (maximum value + minimum value)/2
c) Amplitude = maximum value
d) Amplitude = minimum value - The formula for the general solution of a trigonometric equation is:
a) θ = sin⁻¹(value) + 2πn
b) θ = cos⁻¹(value)+2πn - c) θ = tan⁻¹(value) + πn
- d) θ = value + 2πn
- The formula to convert degrees to radians is:
a) Radians = Degrees × π/180°
b) Radians = Degrees × 180°/π
c) Radians = Degrees/π
d) Radians = Degrees × π - The formula to convert radians to degrees is:
a) Degrees = Radians × π/180°
b) Degrees = Radians × 180°/π
c) Degrees = Radians/π
d) Degrees = Radians × π - The formula for the sum of sine and cosine is:
a) sinθ + cosθ = √2sin(θ + π/4)
b) sinθ + cosθ = √2sin(θ – π/4)
c) sinθ + cosθ = √2cos(θ + π/4)
d) sinθ + cosθ = √2cos(θ – π/4) - The formula for the difference of sine and cosine is:
a) sinθ – cosθ = √2sin(θ + π/4)
b) sinθ – cosθ = √2sin(θ – π/4)
c) sinθ – cosθ = √2cos(θ + π/4)
d) sinθ – cosθ = √2cos(θ – π/4) - The formula for the product of sine and cosine is:
a) sinθcosθ = 0.5sin(2θ)
b) sinθcosθ = 0.5cos(2θ)
c) sinθcosθ = 0.5tan(2θ)
d) sinθcosθ = 0.5cot(2θ) - The formula for the sum of tangents is:
a) tan(α + β) = (tanα + tanβ)/(1 – tanαtanβ)
b) tan(α + β) = tanα + tanβ
c) tan(α + β) = tanα – tanβ
d) tan(α + β) = (tanα – tanβ)/(1 + tanαtanβ) - The formula for the difference of tangents is:
a) tan(α – β) = (tanα – tanβ)/(1 + tanαtanβ)
b) tan(α – β) = tanα + tanβ
c) tan(α – β) = tanα – tanβ
d) tan(α – β) = (tanα + tanβ)/(1 – tanαtanβ) - The formula for the product of tangents is:
a) tanαtanβ = sin(α + β)/(cosαcosβ)
b) tanαtanβ = sin(α – β)/(cosαcosβ)
c) tanαtanβ = cos(α + β)/(sinαsinβ)
d) tanαtanβ = cos(α – β)/(sinαsinβ) - The formula for the quotient of tangents is:
a) tan(α/β) = (tanα + tanβ)/(1 – tanαtanβ)
b) tan(α/β) = (tanα – tanβ)/(1 + tanαtanβ)
c) tan(α/β) = (sinα + sinβ)/(cos
α + cosβ)
d) tan(α/β) = (sinα – sinβ)/(cosα – cosβ)
- The formula for the sum of secant and cosecant is:
a) secθ + cscθ = sec(θ + π/4)
b) secθ + cscθ = sec(θ – π/4)
c) secθ + cscθ = csc(θ + π/4)
d) secθ + cscθ = csc(θ – π/4) - The formula for the difference of secant and cosecant is:
a) secθ – cscθ = sec(θ + π/4)
b) secθ – cscθ = sec(θ – π/4)
c) secθ – cscθ = csc(θ + π/4)
d) secθ – cscθ = csc(θ – π/4) - The formula for the product of secant and cosecant is:
a) secθcscθ = 1
b) secθcscθ = cosθsinθ
c) secθcscθ = cosθ/sinθ
d) secθcscθ = sinθ/cosθ - The formula for the sum of cotangents is:
a) cot(α + β) = (cotαcotβ – 1)/(cotα + cotβ)
b) cot(α + β) = cotα + cotβ
c) cot(α + β) = cotα – cotβ
d) cot(α + β) = (cotα + cotβ)/(cotαcotβ – 1) - The formula for the difference of cotangents is:
a) cot(α – β) = (cotαcotβ + 1)/(cotα – cotβ)
b) cot(α – β) = cotα + cotβ
c) cot(α – β) = cotα – cotβ
d) cot(α – β) = (cotα – cotβ)/(cotαcotβ + 1) - The formula for the product of cotangents is:
a) cotαcotβ = (cotα + cotβ)/(1 – cotαcotβ)
b) cotαcotβ = (cotα – cotβ)/(1 + cotαcotβ)
c) cotαcotβ = (cotα + cotβ)/(cotα – cotβ)
d) cotαcotβ = (cotα – cotβ)/(cotα + cotβ) - The formula for the quotient of cotangents is:
a) cot(α/β) = (cotαcotβ + 1)/(cotα – cotβ)
b) cot(α/β) = (cotαcotβ – 1)/(cotα + cotβ)
c) cot(α/β) = (cotα + cotβ)/(cotα + cotβ)
d) cot(α/β) = (cotα – cotβ)/(cotα – cotβ) - The formula for the sum of cosecant and secant is:
a) cscθ + secθ = csc(θ + π/4)
b) cscθ + secθ = csc(θ – π/4)
c) cscθ + secθ = sec(θ + π/4)
d) cscθ + secθ = sec(θ – π/4) - The formula for the difference of cosecant and secant is:
a) cscθ – secθ = csc(θ + π/4)
b) cscθ – secθ = csc(θ – π/4)
c) cscθ – secθ = sec(θ + π/4)
d) cscθ – secθ = sec(θ – π/4) - The formula for the product of cosecant and secant is:
a) cscθsecθ = 1
b) cscθsecθ = cscθ/sinθ
c) cscθsecθ = cosθ/sinθ
d) cscθsecθ = sinθ/cosθ - The formula for the sum of cotangent and tangent is:
a) cotθ + tanθ = cot(θ + π/4)
b) cotθ + tanθ = cot(θ – π/4)
c) cotθ + tanθ = tan(θ + π/4)
d) cotθ + tanθ = tan(θ – π/4) - The formula for the difference of cotangent and tangent is:
a) cotθ – tanθ = cot(θ + π/4)
b) cotθ – tanθ = cot(θ – π/4)
c) cotθ – tanθ = tan(θ + π/4)
d) cotθ – tanθ = tan(θ – π/4) - The formula for the product of cotangent and tangent is:
a) cotθtanθ = 1
b) cotθtanθ = cotθ/tanθ
c) cotθtanθ = tanθ/cotθ
d) cotθtanθ = tanθ × cotθ - The formula for the sum of cosecant and sine is:
a) cscθ + sinθ = csc(θ + π/4)
b) cscθ + sinθ = csc(θ – π/4)
c) cscθ + sinθ = sin(θ + π/4)
d) cscθ + sinθ = sin(θ – π/4) - The formula for the difference of cosecant and sine is:
a) cscθ – sinθ = csc(θ + π/4)
b) cscθ – sinθ = csc(θ – π/4)
c) cscθ – sinθ = sin(θ + π/4)
d) cscθ – sinθ = sin(θ – π/4) - The formula for the product of cosecant and sine is:
a) cscθsinθ = 1
b) cscθsinθ = cscθ/sinθ
c) cscθsinθ = sinθ/cscθ
d) cscθsinθ = sin²θ - The formula for the sum of secant and cosine is:
a) secθ + cosθ = sec(θ + π/4)
b) secθ + cosθ = sec(θ – π/4)
c) secθ + cosθ = cos(θ + π/4)
d) secθ + cosθ = cos(θ – π/4) - The formula for the difference of secant and cosine is:
a) secθ – cosθ = sec(θ + π/4)
b) secθ – cosθ = sec(θ – π/4)
c) secθ – cosθ = cos(θ + π/4)
d) secθ – cosθ = cos(θ – π/4) - The formula for the product of secant and cosine is:
a) secθcosθ = 1
b) secθcosθ = secθ/cosθ
c) secθcosθ = cosθ/secθ
d) secθcosθ = cos²θ - The formula for the sum of cosecant and cosine is:
a) cscθ + cosθ = csc(θ + π/4)
b) cscθ + cosθ = csc(θ – π/4)
c) cscθ + cosθ = cos(θ + π/4)
d) cscθ + cosθ = cos(θ – π/4)
Note: Please note that these are just a few examples of formulas in trigonometry. There are many more formulas and identities that exist in the subject.
https://impetusgurukull.com/category/us-big-newz/
https://www.impetusgurukul.com/
